NGHIÊN CỨU GIẢI THUẬT DI TRUYỀN VỚI BIẾN LIÊN TỤC CHO BÀI TOÁN TÌM CỰC TRỊ CỦA HÀM SỐ

Dương Trung Nguyện

Trung tâm Thực hành - Thí nghiệm, Trường Đại học Vinh

Tóm tắt: Trong công trình này nhóm tác giả đã tập trung nghiên cứu giải thuật di truyền. Giải thuật di truyền được xem là công cụ hiệu quả để giải quyết bài toán tối ưu, đầu tiên là bài toán tìm cực trị của hàm số, đã được các nhà nghiên cứu quan tâm khá sớm. Trong thực tế, các biến thường là các biến liên tục, khi đó, việc mã hóa các biến sử dụng trong việc tính toán các toán tử của GA là vấn đề đặt ra. Tác giả đã sử dụng ngôn ngữ lập trình Matlab để cài đặt hệ thống, lập trình các thuật toán trên máy tính và đánh giá hiệu quả của các thuật toán. Luận văn có ý nghĩa khoa học và thực tiễn.

1. Mở đầu

Trong ngành khoa học máy tính,  tìm kiếm lời giải tối ưu cho các bài  toán là vấn đề được các nhà khoa học máy tính đặc biệt quan tâm. Mục đích chính của các thuật toán tìm kiếm lời giải là tìm ra lời giải tối ưu cho bài toán trong thời gian nhỏ nhất. Thuật giải di truyền đã được phát minh ra để bắt chước quá trình phát triển tự nhiên trong điều kiện quy định sẵn của môi trường. Các đặc điểm của quá trình này đã thu hút sự chú ý của John Holand (ở đại học Michigan) ngay từ những năm 1970. Holand tin rằng sự gắn kết thích hợp trong thuật giải máy tính có thể tạo ra một kỹ thuật giúp giải quyết các vấn đề khó khăn giống như trong tự nhiên đã diễn ra thông qua quá trình tiến hóa.

Hiện nay có rất nhiều phương pháp giải quyết bài toán tối ưu hàm số, nhưng các phương pháp chỉ dừng lại ở những lớp bài toán với những thông tin không rõ ràng. Do đó, việc tìm ra một phương pháp mới để giải quyết bài toán tối ưu hàm nhiều biến tổng quát là cần thiết. Xuất phát từ vấn đề này, công trình nghiên cứu của tác giả Dương Trung Nguyện dưới sự hướng dẫn khoa học của TS. Hoàng Hữu Việt đã hướng tới một giải pháp tối ưu để giải quyết bài toán.

2. Tóm lược kết quả nghiên cứu

Các kết quả của công trình có thể tóm lược ở các nội dung chính sau đây:

1. Tổng quan về bài toán tìm cực trị của hàm số, cơ sở toán học, các phương pháp cơ bản tìm cực trị của hàm số gồm thuật toán vét cạn, thuật toán tìm kiếm cục bộ và giải thuật di truyền.

2. Giới thiệu đại cương về giải thuật di truyền, trình bày các bước chủ yếu của giải thuật di truyền nhị phân, tìm hiểu các ví dụ về giải thuật di truyền với biến nhị phân.

3. Giải thuật di truyền với biến liên tục cho bài toán tìm cực trị của hàm số. Trình bày Giải thuật di truyền với biến liên tục, cài đặt giải thuật di truyền cho bài toán tìm cực trị hàm số và đánh giá hiệu quả của giải thuật bằng thực nghiệm.

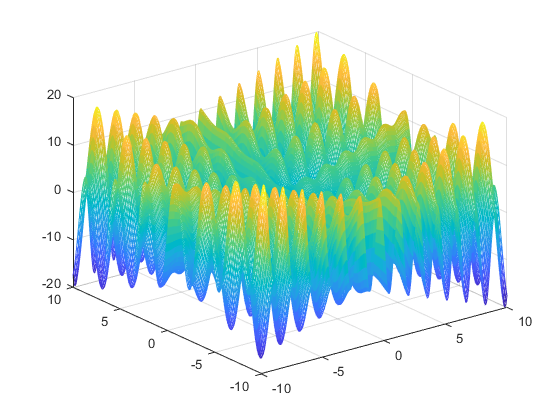
a) Hàm f₁(x,y)

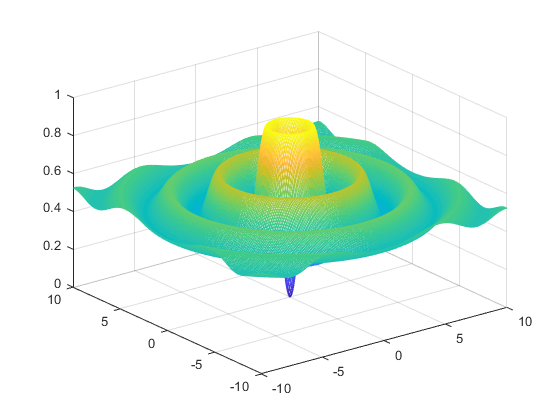
b) Hàm f₂(x,y)

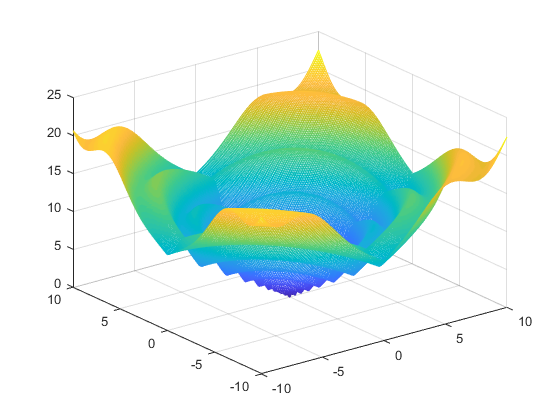
c) Hàm f₃(x,y)

d) Hàm f₄(x,y)

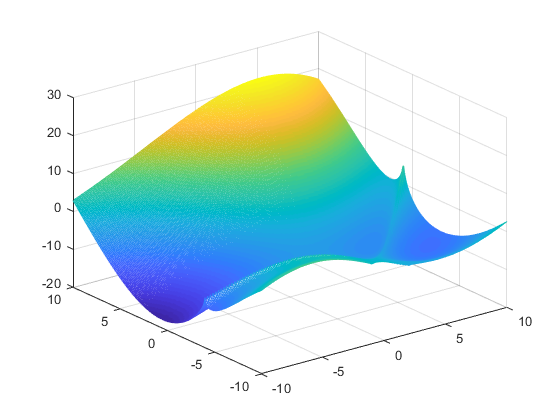
e) Hàm f₅(x,y)

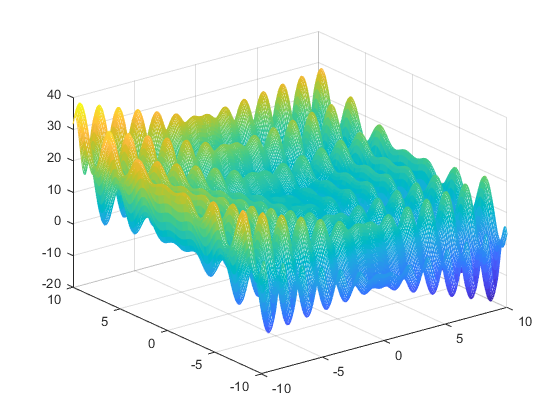
f) Hàm f₆(x,y)

Hình ảnh đồ thị của các hàm số

3. Kết luận